面向 3D 盒子的交并比：一种新算法

作者：Georgia Gkioxari

实现：Georgia Gkioxari 和 Nikhila Ravi

描述

盒子的交并比 (IoU) 广泛用作目标检测中的评估指标（1，2）。在 2D 中，IoU 通常应用于轴对齐的盒子，即边缘平行于图像轴的盒子。在 3D 中，盒子通常不是轴对齐的，并且可以以任何方式在世界中定向。我们引入了一种新算法，该算法计算两个面向 3D 盒子的精确 IoU。

我们的算法基于一个简单的观察结果，即两个面向 3D 盒子 box1 和 box2 的交集是一个凸多面体（2D 中的凸 n 边形），其中 n > 2 由连接的平面单元组成。在 3D 中，这些平面单元是 3D 三角面。在 2D 中，它们是 2D 边缘。每个平面单元严格属于 box1 或 box2。我们的算法通过迭代每个盒子的边来找到这些单元。

  1. 对于 box1 中的每个 3D 三角面 e，我们检查 e 是否在 box2 内部。
  2. 如果 e 不在内部，则将其丢弃。
  3. 如果 e 在内部或部分在内部，则 box2 内部的 e 部分将添加到构成最终交集形状的单元中。
  4. 我们对 box2 重复此操作。

下面，我们展示了我们算法在 2D 面向盒子的情况下的可视化。

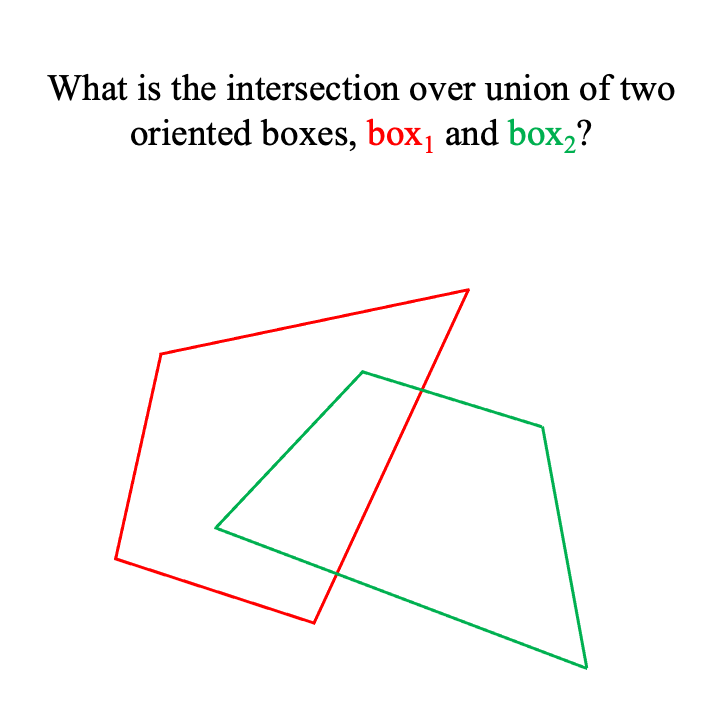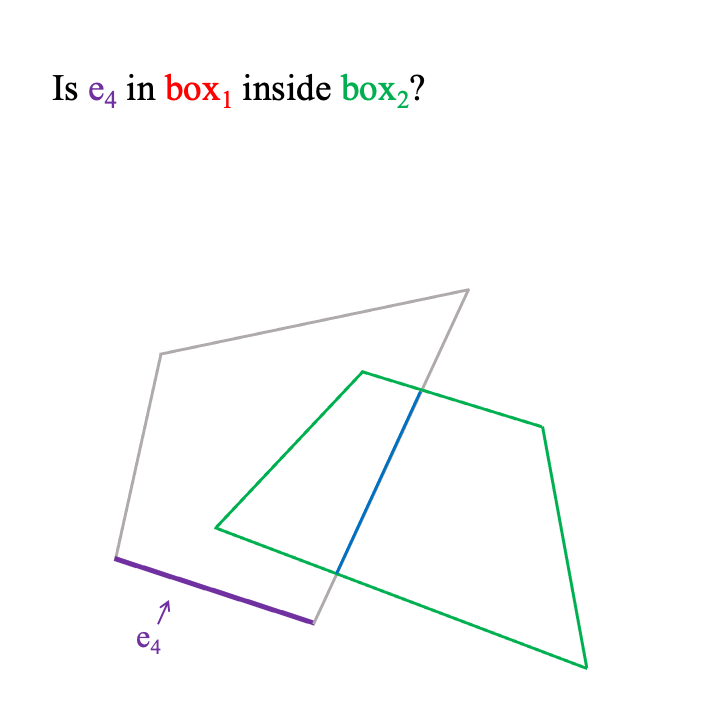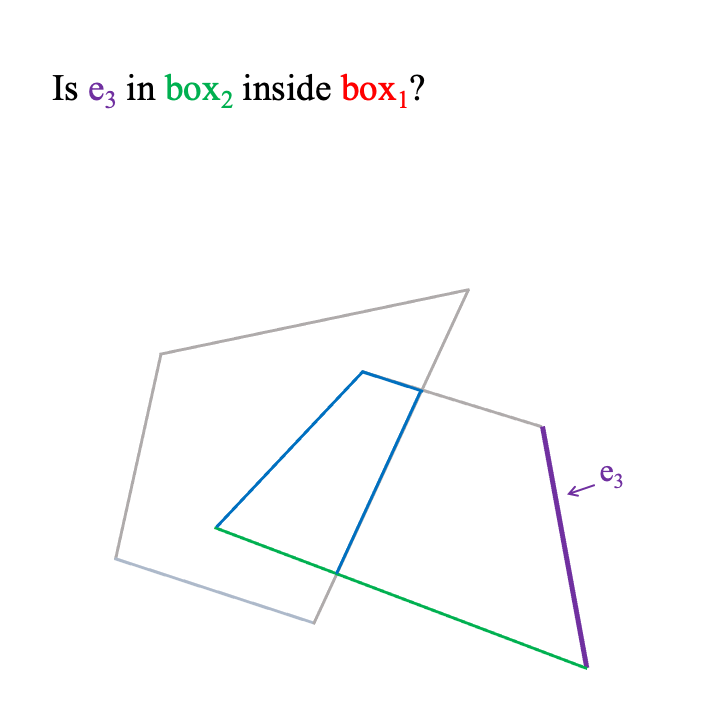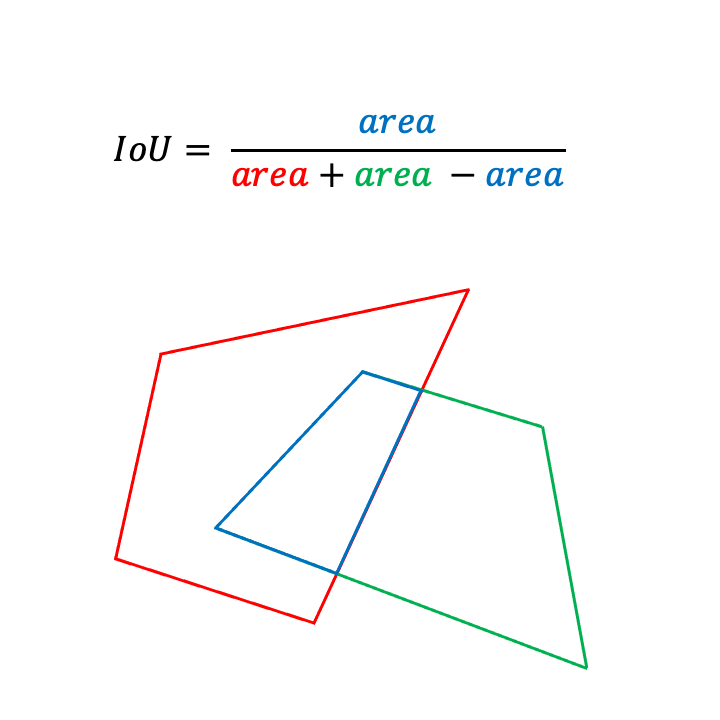
drawing

请注意，当盒子的单元 e 部分在内部 box 时，e 会分解成更小的单元。在 2D 中，e 是一个边缘，并分解成更小的边缘。在 3D 中，e 是一个 3D 三角面，并且被它与之相交的 box 的平面裁剪成更多更小的面。这是 2D 和 3D 算法之间唯一的根本区别。

与其他算法的比较

当前用于 3D 盒子 IoU 的算法依赖于粗略的近似值或做出盒子假设，例如，它们限制了 3D 盒子的方向。Objectron 对先前工作的局限性进行了很好的讨论。Objectron 引入了一种用于面向 3D 盒子的精确 IoU 计算的优秀算法。Objectron 的算法使用Sutherland-Hodgman 算法计算两个盒子的交点。交集形状由交点的凸包形成，使用Qhull 库。

我们的算法相对于 Objectron 的算法有几个优点

  • 我们的算法也计算交点，类似于 Objectron，但此外还存储点所属的平面单元。这消除了对凸包计算的需要，凸包计算为 O(nlogn) 并依赖于第三方库，该库通常会以无法描述的错误消息崩溃。
  • Objectron 的实现假设盒子与轴对齐之间存在旋转关系。我们的算法和实现没有这样的假设，适用于任何 3D 盒子。
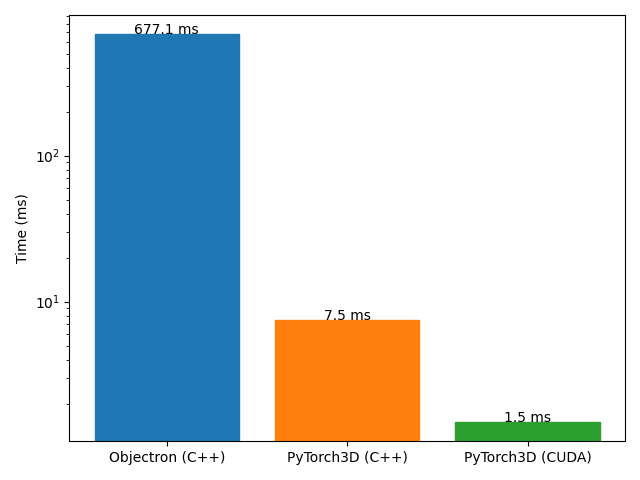
  • 我们的实现支持批处理，而 Objectron 假设 box1 和 box2 的输入为单个元素。
  • 我们的实现易于并行化，事实上，我们提供了一个自定义的 C++/CUDA 实现，其速度比 Objectron 快 450 倍。

下面我们比较了 Objectron（使用 C++）和我们的算法（使用 C++ 和 CUDA）的性能。我们针对目标检测中的一个常见用例进行基准测试，其中 boxes1 包含 M 个预测，boxes2 包含图像中 N 个地面实况 3D 盒子，并计算 MxN IoU 矩阵。我们报告 M=N=16 的时间（以毫秒为单位）。

drawing

用法和代码

from pytorch3d.ops import box3d_overlap
# Assume inputs: boxes1 (M, 8, 3) and boxes2 (N, 8, 3)
intersection_vol, iou_3d = box3d_overlap(boxes1, boxes2)

有关更多详细信息，请阅读iou_box3d.py。

请注意，我们的实现目前不可微。我们计划尽快添加梯度支持。

我们还包括了广泛的测试，将我们的实现与 Objectron 和 MeshLab 进行比较。

引用

如果您使用我们的 3D IoU 算法，请引用 PyTorch3D

@article{ravi2020pytorch3d,
    author = {Nikhila Ravi and Jeremy Reizenstein and David Novotny and Taylor Gordon
                  and Wan-Yen Lo and Justin Johnson and Georgia Gkioxari},
    title = {Accelerating 3D Deep Learning with PyTorch3D},
    journal = {arXiv:2007.08501},
    year = {2020},
}
← CubifyPlotly 可视化 →