在 [ ]

# Copyright (c) Meta Platforms, Inc. and affiliates. All rights reserved.

给定一组相对相机对的绝对相机方向¶

本教程展示了cameras、transforms和so3 API。

我们处理的问题定义如下

给定一个包含$N$个相机的光学系统，其外部参数为$\{g_1, ..., g_N | g_i \in SE(3)\}$，以及一组相对相机位置$\{g_{ij} | g_{ij}\in SE(3)\}$，这些位置映射在随机选择的相机对$(i, j)$的坐标系之间，我们寻找与相对相机运动一致的绝对外部参数$\{g_1, ..., g_N\}$。

更正式地说：$$ g_1, ..., g_N = {\arg \min}_{g_1, ..., g_N} \sum_{g_{ij}} d(g_{ij}, g_i^{-1} g_j), $$, 其中$d(g_i, g_j)$是一个合适的度量，用于比较相机$g_i$和$g_j$的外部参数。

从视觉上看，问题可以描述如下。下图描绘了优化开始时的场景。真实相机以紫色绘制，而随机初始化的估计相机以橙色绘制： Initialization

我们的优化旨在通过最小化相对相机对之间的差异，使估计（橙色）相机与真实（紫色）相机对齐。因此，问题的解决方案应如下所示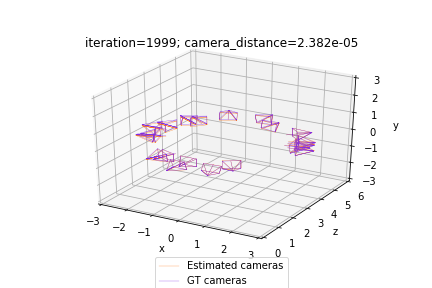： Solution

在实践中，相机外部参数$g_{ij}$和$g_i$使用SfMPerspectiveCameras类的对象表示，这些对象使用相应的旋转和平移矩阵R_absolute和T_absolute初始化，这些矩阵定义了外部参数$g = (R, T); R \in SO(3); T \in \mathbb{R}^3$。为了确保R_absolute是一个有效的旋转矩阵，我们使用旋转的轴角表示log_R_absolute的指数映射（用so3_exp_map实现）来表示它。

请注意，此问题的解决方案只能恢复到一个未知的全局刚性变换$g_{glob} \in SE(3)$。因此，为简单起见，我们假设已知第一个相机$g_0$的绝对外部参数。我们将$g_0$设置为一个平凡的相机$g_0 = (I, \vec{0})$。

0. 安装和导入模块¶

确保已安装torch和torchvision。如果未安装pytorch3d，请使用以下单元格安装它

在 [ ]

import os
import sys
import torch
need_pytorch3d=False
try:
    import pytorch3d
except ModuleNotFoundError:
    need_pytorch3d=True
if need_pytorch3d:
    if torch.__version__.startswith("2.2.") and sys.platform.startswith("linux"):
        # We try to install PyTorch3D via a released wheel.
        pyt_version_str=torch.__version__.split("+")[0].replace(".", "")
        version_str="".join([
            f"py3{sys.version_info.minor}_cu",
            torch.version.cuda.replace(".",""),
            f"_pyt{pyt_version_str}"
        ])
        !pip install fvcore iopath
        !pip install --no-index --no-cache-dir pytorch3d -f https://dl.fbaipublicfiles.com/pytorch3d/packaging/wheels/{version_str}/download.html
    else:
        # We try to install PyTorch3D from source.
        !pip install 'git+https://github.com/facebookresearch/pytorch3d.git@stable'

在 [ ]

# imports
import torch
from pytorch3d.transforms.so3 import (
    so3_exp_map,
    so3_relative_angle,
)
from pytorch3d.renderer.cameras import (
    SfMPerspectiveCameras,
)

# add path for demo utils
import sys
import os
sys.path.append(os.path.abspath(''))

# set for reproducibility
torch.manual_seed(42)
if torch.cuda.is_available():
    device = torch.device("cuda:0")
else:
    device = torch.device("cpu")
    print("WARNING: CPU only, this will be slow!")

如果使用Google Colab，请获取用于绘制相机场景的实用程序文件以及真实相机位置

在 [ ]

!wget https://raw.githubusercontent.com/facebookresearch/pytorch3d/main/docs/tutorials/utils/camera_visualization.py
from camera_visualization import plot_camera_scene

!mkdir data
!wget -P data https://raw.githubusercontent.com/facebookresearch/pytorch3d/main/docs/tutorials/data/camera_graph.pth

或者，如果本地运行，请取消注释并运行以下单元格

在 [ ]

# from utils import plot_camera_scene

1. 设置相机并加载真实位置¶

在 [ ]

# load the SE3 graph of relative/absolute camera positions
camera_graph_file = './data/camera_graph.pth'
(R_absolute_gt, T_absolute_gt), \
    (R_relative, T_relative), \
    relative_edges = \
        torch.load(camera_graph_file)

# create the relative cameras
cameras_relative = SfMPerspectiveCameras(
    R = R_relative.to(device),
    T = T_relative.to(device),
    device = device,
)

# create the absolute ground truth cameras
cameras_absolute_gt = SfMPerspectiveCameras(
    R = R_absolute_gt.to(device),
    T = T_absolute_gt.to(device),
    device = device,
)

# the number of absolute camera positions
N = R_absolute_gt.shape[0]

2. 定义优化函数¶

相对相机和相机距离¶

我们现在定义两个对优化至关重要的函数。

calc_camera_distance比较一对相机。此函数很重要，因为它定义了我们正在最小化的损失。该方法利用了SO3 API中的so3_relative_angle函数。

get_relative_camera计算映射在一对绝对相机之间的相对相机的参数。在这里，我们利用了PyTorch3D Transforms API中的compose和inverse类方法。

在 [ ]

def calc_camera_distance(cam_1, cam_2):
    """
    Calculates the divergence of a batch of pairs of cameras cam_1, cam_2.
    The distance is composed of the cosine of the relative angle between 
    the rotation components of the camera extrinsics and the l2 distance
    between the translation vectors.
    """
    # rotation distance
    R_distance = (1.-so3_relative_angle(cam_1.R, cam_2.R, cos_angle=True)).mean()
    # translation distance
    T_distance = ((cam_1.T - cam_2.T)**2).sum(1).mean()
    # the final distance is the sum
    return R_distance + T_distance

def get_relative_camera(cams, edges):
    """
    For each pair of indices (i,j) in "edges" generate a camera
    that maps from the coordinates of the camera cams[i] to 
    the coordinates of the camera cams[j]
    """

    # first generate the world-to-view Transform3d objects of each 
    # camera pair (i, j) according to the edges argument
    trans_i, trans_j = [
        SfMPerspectiveCameras(
            R = cams.R[edges[:, i]],
            T = cams.T[edges[:, i]],
            device = device,
        ).get_world_to_view_transform()
         for i in (0, 1)
    ]
    
    # compose the relative transformation as g_i^{-1} g_j
    trans_rel = trans_i.inverse().compose(trans_j)
    
    # generate a camera from the relative transform
    matrix_rel = trans_rel.get_matrix()
    cams_relative = SfMPerspectiveCameras(
                        R = matrix_rel[:, :3, :3],
                        T = matrix_rel[:, 3, :3],
                        device = device,
                    )
    return cams_relative

3. 优化¶

最后，我们开始优化绝对相机。

我们使用带动量的SGD，并对log_R_absolute和T_absolute进行优化。

如前所述，log_R_absolute是我们绝对相机的旋转部分的轴角表示。我们可以使用以下方法获得对应于log_R_absolute的3x3旋转矩阵R_absolute：

R_absolute = so3_exp_map(log_R_absolute)

在 [ ]

# initialize the absolute log-rotations/translations with random entries
log_R_absolute_init = torch.randn(N, 3, dtype=torch.float32, device=device)
T_absolute_init = torch.randn(N, 3, dtype=torch.float32, device=device)

# furthermore, we know that the first camera is a trivial one 
#    (see the description above)
log_R_absolute_init[0, :] = 0.
T_absolute_init[0, :] = 0.

# instantiate a copy of the initialization of log_R / T
log_R_absolute = log_R_absolute_init.clone().detach()
log_R_absolute.requires_grad = True
T_absolute = T_absolute_init.clone().detach()
T_absolute.requires_grad = True

# the mask the specifies which cameras are going to be optimized
#     (since we know the first camera is already correct, 
#      we only optimize over the 2nd-to-last cameras)
camera_mask = torch.ones(N, 1, dtype=torch.float32, device=device)
camera_mask[0] = 0.

# init the optimizer
optimizer = torch.optim.SGD([log_R_absolute, T_absolute], lr=.1, momentum=0.9)

# run the optimization
n_iter = 2000  # fix the number of iterations
for it in range(n_iter):
    # re-init the optimizer gradients
    optimizer.zero_grad()

    # compute the absolute camera rotations as 
    # an exponential map of the logarithms (=axis-angles)
    # of the absolute rotations
    R_absolute = so3_exp_map(log_R_absolute * camera_mask)

    # get the current absolute cameras
    cameras_absolute = SfMPerspectiveCameras(
        R = R_absolute,
        T = T_absolute * camera_mask,
        device = device,
    )

    # compute the relative cameras as a composition of the absolute cameras
    cameras_relative_composed = \
        get_relative_camera(cameras_absolute, relative_edges)

    # compare the composed cameras with the ground truth relative cameras
    # camera_distance corresponds to $d$ from the description
    camera_distance = \
        calc_camera_distance(cameras_relative_composed, cameras_relative)

    # our loss function is the camera_distance
    camera_distance.backward()
    
    # apply the gradients
    optimizer.step()

    # plot and print status message
    if it % 200==0 or it==n_iter-1:
        status = 'iteration=%3d; camera_distance=%1.3e' % (it, camera_distance)
        plot_camera_scene(cameras_absolute, cameras_absolute_gt, status)

print('Optimization finished.')

4. 结论¶

在本教程中，我们学习了如何初始化一批SfM相机、为捆绑调整设置损失函数以及运行优化循环。